Data Construction and Algorithms Class
Practice Problems on Divide and Conquer
Recent Articles on Divide and Conquer

What is Divide and Conquer?

Divide and Conquer is an algorithmic epitome in which the trouble is solved using the Split, Conquer, and Combine strategy.

A typical Divide and Conquer algorithm solves a trouble using following three steps:

  1. Separate: This involves dividing the trouble into smaller sub-problems.
  2. Conquer: Solve sub-problems by calling recursively until solved.
  3. Combine: Combine the sub-problems to become the last solution of the whole problem.

Standard algorithms that follow Divide and Conquer algorithm

The following are some standard algorithms that follow Divide and Conquer algorithm.

  1. Quicksort is a sorting algorithm. The algorithm picks a pivot element and rearranges the array elements so that all elements smaller than the picked pivot element move to the left side of the pivot, and all greater elements move to the right side. Finally, the algorithm recursively sorts the subarrays on the left and right of the pivot element.
  2. Merge Sort is also a sorting algorithm. The algorithm divides the assortment into two halves, recursively sorts them, and finally merges the ii sorted halves.
  3. Closest Pair of Points The problem is to find the closest pair of points in a prepare of points in the x-y aeroplane. The problem tin exist solved in O(n^two) time by calculating the distances of every pair of points and comparing the distances to find the minimum. The Divide and Conquer algorithm solves the problem in O(N log N) fourth dimension.
  4. Strassen's Algorithm is an efficient algorithm to multiply two matrices. A simple method to multiply two matrices needs 3 nested loops and is O(n^iii). Strassen's algorithm multiplies 2 matrices in O(n^2.8974) time.
  5. Cooley–Tukey Fast Fourier Transform (FFT) algorithm is the most common algorithm for FFT. It is a carve up and conquer algorithm which works in O(N log N) fourth dimension.
  6. Karatsuba algorithm for fast multiplication does the multiplication of two due north-digit numbers in at most 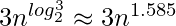3n^{log_{2}^{3}}\approx 3n^{1.585} single-digit multiplications in full general (and exactlyn^{\log_23} when northward is a ability of 2). It is, therefore, faster than the classical algorithm, which requires n 2 unmarried-digit products. If n = 210 = 1024, in detail, the exact counts are threeten = 59, 049 and (ii10)2 = 1, 048, 576, respectively.

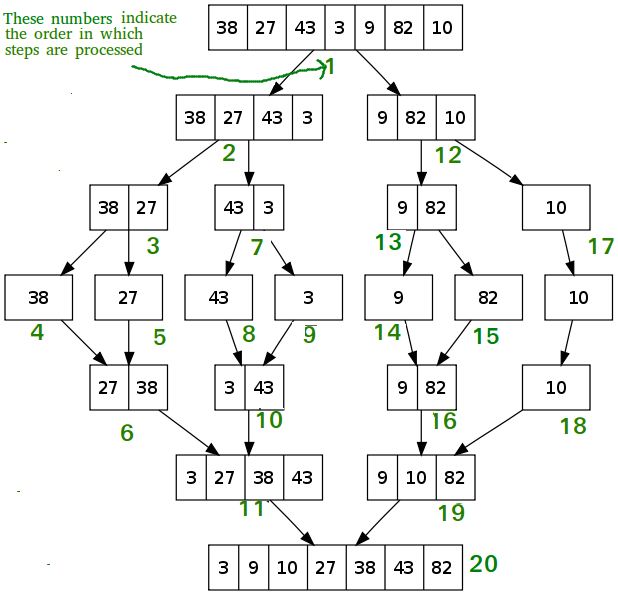
Example of Separate and Conquer algorithm

A classic example of Separate and Conquer is Merge Sort demonstrated below. In Merge Sort, we divide assortment into two halves, sort the ii halves recursively, and then merge the sorted halves.
Merge-Sort-Tutorial

Topics :

  • Standard Algorithms
  • Binary Search Based
  • Misc
  • Quick Links

Standard Algorithms :

  1. Intoduction to Separate and Conquer
  2. Binary Search
  3. Randomized Binary Search Algorithm
  4. Merge Sort
  5. Quick Sort
  6. Tiling Trouble
  7. Count Inversions
  8. Summate pow(ten, due north)
  9. Closest Pair of Points
  10. Closest Pair of Points | O(nlogn) Implementation
  11. Multiply two polynomials
  12. Strassen's Matrix Multiplication
  13. The Skyline Problem
  14. Maximum Subarray Sum
  15. Longest Mutual Prefix
  16. Search in a Row-wise and Cavalcade-wise Sorted 2D Array
  17. Karatsuba algorithm for fast multiplication
  18. Convex Hull (Simple Divide and Conquer Algorithm)
  19. Quickhull Algorithm for Convex Hull
  20. Distinct elements in subarray using Mo's Algorithm

    21. DSA-Self-Paced

Binary Search Based :

  1. Median of 2 sorted arrays
  2. Median of two sorted arrays of different sizes
  3. Floor in a Sorted Array
  4. Find closest number in array
  5. Find a Stock-still Signal in a given arrray
  6. Find a superlative element in a given assortment
  7. Check for Majority Chemical element in a sorted array
  8. 1000-thursday Element of Two Sorted Arrays
  9. Detect the Rotation Count in Rotated Sorted array
  10. Find the minimum chemical element in a sorted and rotated array
  11. Find the only repeating element in a sorted assortment of size n
  12. Discover alphabetize of an actress chemical element present in one sorted array
  13. Find the element that appears one time in a sorted array
  14. Count number of occurrences (or frequency) in a sorted array
  15. Observe the maximum element in an assortment which is first increasing and so decreasing
  16. Subtract and Conquer
  17. Binary Search using pthread
  18. Binary Search on Singly Linked List
  19. The painter's partition problem
  20. The painter's partition problem | Set up 2
  21. Observe the number of zeroes
  22. Numbers whose factorials end with n zeros
  23. Observe the missing number in Arithmetic Progression
  24. Number of days after which tank will become empty
  25. Find bitonic point in given bitonic sequence
  26. Detect the point where a monotonically increasing part becomes positive first time

Misc :

  1. Iterative Tower of Hanoi
  2. Program for Tower of Hanoi
  3. Foursquare root of an integer
  4. Discover cubic root of a number
  5. Allocate minimum number of pages
  6. Collect all coins in minimum number of steps
  7. Modular Exponentiation (Power in Modular Arithmetic)
  8. Find a peak element in a 2D array
  9. Program to count number of set bits in an (large) array
  10. Maximum and minimum of an array using minimum number of comparisons
  11. Find frequency of each element in a limited range array in less than O(northward) time
  12. Minimum deviation between adjacent elements of array which comprise elements from each row of a matrix
  13. Search element in a sorted matrix
  14. Piece of cake manner to think Strassen's Matrix Equation
  15. Largest Rectangular Area in a Histogram | Set 1
  16. Advanced master theorem for divide and conquer recurrences
  17. Identify k elements such that minimum distance is maximized
  18. Iterative Fast Fourier Transformation for polynomial multiplication
  19. Write you own Power without using multiplication(*) and division(/) operators
  20. Sequences of given length where every element is more than than or equal to twice of previous
  21. Shuffle 2n integers in format {a1, b1, a2, b2, a3, b3, ……, an, bn} without using actress space

Quick Links :

  • 'Practice Bug' on Divide and Conquer
  • 'Quizzes' on Divide and Conquer

If yous like GeeksforGeeks and would similar to contribute, you can also write an article and mail service your commodity to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if yous discover anything wrong, or y'all want to share more than data about the topic discussed to a higher place.